[논문리뷰]Dynamic Graph CNN for Learning on Point Clouds

카테고리 없음

[논문리뷰]Dynamic Graph CNN for Learning on Point Clouds

Local Feature 2024. 7. 31. 11:03

Introduction

point cloud는 컴퓨터 그래픽스 분야에서 많이 사용되지만 topological information을 표현하는 기술은 발전되기 어렵다.
topological : 물리적인 배치의 형태로 이루어진 현장의 종류
→ point cloud의 point를 물리적인 배치의 형태로 표현하고 컴퓨터에 인식한다.

PointNet++는 계층적 구조를 도입하여 local feature를 추출하려고 하였으나 point 간의 기하학적 관계를 무시하기 때문에 local feature를 포착하는데 한계를 가지고있다.
EdgeConv라는 새로운 알고리즘을 제안하며 point와 이웃한 point의 관계를 설명하는 방법론 제시
- EdgeConv는 이웃의 순서에 대해 불변하기 때문에 permutation invarance하다.
- point간의 local graph를 구성하고 가장자리에 대한 embedding을 학습한다.
⇒ 유클리드 공간과 sementic 공간에서 모두 point를 그룹화할 수 있다.
DGCNN은 permutation invarance를 유지하며 point간의 local feature를 학습할 수 있고 layer 간 그래프를 동적으로 업데이트하며 기존 Point cloud 처리 네트워크에 EdgeConv를 통합할 수 있다는 기여점을 가진다.

Related Work

variational autoencoder와 autoencoder, GAN과의 차이
- input과 output 사이에 vertices가 없다는 점이다. (정형화된 형식이 주어지지 않기 때문에 input과 output의 순서에 대해 강건해야함)
- point cloud의 point 3개를 연결한 가장 작은 단위인 mesh가 주어지고 그 vertices가 정형화된 형식으로 주어지지 않음

Our Approach

PointNet과 CNN에서 아이디어를 얻은 접근 방식을 제안하였으나 개별 point에 집중하는 것이 아닌 각 point를 노드로 생각하여 graph network의 관련성에 따라 local neighborhood graph를 구성하고 인접한 point pair를 연결하는 edge에 CNN 연산을 적용하여 활용한다.
이후 Edge Conv라는 알고리즘이 translation-invariance와 non-locality의 특징을 가진다.
graph CNN과 달리 graph가 고정되어 있지 않고 network의 각 layer마다 동적으로 업데이트된다. → 매 layer를 통과할 때마다 새로 sequence of embedding을 계산한다. → k-nn에 해당하는 점들의 집합이 변경된다.

전체적으로 PointNet과 유사한 구조를 가지고 있다.
EdgeConv를 거칠 때마다 skip link connection이 max pooling을 적용시키기 전 단계에 정보를 저장한다.
point cloud 변환 블록은 (3, 3)행렬을 적용하여 입력된 point cloud를 정렬하도록 설계되었다. (3, 3)행렬을 적용시키기 위해 각 point의 좌표와 인접한 k개 점 사이의 좌표 차이를 연결하는 tensor가 사용된다.
EdgeConv 블록은 (n, f) 형태의 tensor를 입력으로 받아 layer 뉴런의 수가 $\{a_1, a_2,\dots, a_n\}$으로 정의된 레이어 뉴런 수를 정의하고 인접한 Edge feature 간에 pooling 한 후 $(n, a_n)$ 형태의 tensor를 생성한다.

Edge Convolution

유클리드 공간에서 정의가능한 좌표들인 $x$로 표현되고 특징은 $F$개를 가진다. $F$의 최소값은 3이고 ($x, y, z$좌표) 4 이상일 때는 채널, 표면 정보가 포함될 수 있다. 나중에 오는 layer는 이전 layer에 대한 영향을 받기 때문에 항상 변한다.

local point cloud structure를 계산하기 위해 $G=(V,E)$로 나타낸다.
V는 point들의 집합인 $\{1,\dots,n\}$으로 나타낼 수 있고 E는 V와 V의 관계로 나타낼 수 있다.
가장 간단한 경우 G는 유클리드 공간에서의 X의 k-nn 그래프로 구성된다.

G에는 self-loop또한 포함되어 있어 각 노드가 자신을 가리키기도 한다.
Edge feature를 $e_{ij}=h_\Theta(x_i,x_j)$로 정의하고 $h_\Theta:\mathbb{R}^F\times \mathbb{R}^F$이다. $\Theta$는 학습 가능한 파라미터이다.
각 노드에서 나오는 모든 edge와 관련된 edge feature에 channel-wise symmetric aggregation 연산을 적용하여 EdgeConv 연산을 정의한다.
i번째 노드에서 EdgeConv의 출력은

$$ x'i=\square{j:(i, j)\in \varepsilon} h_{\Theta}(x_i, x_j) $$

과 같이 주어진다.

이미지를 따라서 convolution 연산을 하는 것과 유사하게 $x_i$를 중심 픽셀로 간주하고 ${j:(i, j)\in \varepsilon}$를 주변의 패치로 간주한다.
전체적으로 n개의 점을 가진 point cloud가 주어지면 EdgeConv는 동일한 수의 점을 가진 F차원 point cloud를 생성한다.
첫번째 선택 $h, \square$
- edge function과 집계 연산은 EdgeConv의 속성에 영향을 끼친다.
- 모든 점이 규칙적인 격자(이미지 픽셀)를 나타내고 G가 각 픽셀 주위에 고정된 패치를 나타내는 연결성을 갖는 경우 edge 함수는 $\theta_m\cdot x_j$로 나타내고 집계 연산은 $\sum$을 사용한다.
$$ x'{im}=\sum{j:(i, j)\in \varepsilon}\theta_m \cdot x_{j\cdot} $$
- 여기서 $\theta=(\theta_1,\dots,\theta_M)$은 M개의 서로 다른 필터의 가중치를 인코딩한다.(sharp filter, laplacian filter, blur filter)이고 $\cdot$는 유클리드 내적(dot product)을 나타낸다.
두번째 선택
- h는 local neighbor structure를 무시하고 global feature만 인코딩한다.
- PointNet에서 사용되는 edge function으로 symmetric function과 같다.
$$ h_{\Theta}(x_i, x_j)=h_{\Theta}(x_j) $$
세번째 선택
- PCNN 모델에서 채택한 edge function이다.
- $g$는 가우스 커널, $u$는 유클리드 공간에서의 pairwise distance 거리를 계산한다.
$$ x'{im}=\sum{j\in \mathcal V}(h_{\theta(x_j)})g(u(x_i, x_j)) $$
가우시안 커널 : 유클리드 공간에서의 가까이 있는 point에 더 가중치를 많이 두는 방식이다. local feature는 잘 포착할 수 있으나 global feature는 쉽게 포착할 수 없다.
네번째 선택
- 각 점들의 local feature만 계산하는 구조로 전역적인 정보를 포착할 수 없다.
$$ h_{\Theta}(x_i,x_j)=h_{\Theta}(x_j-x_i) $$
DGCNN에서 채택한 방법 - 비대칭 함수
- PointNet 계열의 point patch 중심 global feature struction과 네 번째 방식으로 추출한 local neighbor sturction 정보를 결합한다.
- maxpooling을 위한 EdgeConv의 연산자로
$$ e_{ijm}=\text{ReLU}(\theta_m \cdot (x_j-x_i)+\phi_m \cdot x_i) $$
- 을 정의할 수 있다.
- 해당 연산자를 통해 $\Theta=(\theta_1, \dots, \theta_M,\phi_1,\dots,\phi_M)$인 maxpooling을 계산할 수 있다.
$$ h_\Theta(x_i, x_j)=\bar{h}_\Theta(x_i, x_j-x_i) $$

Dynamic Graph

실험 결과 각 layer에서 생성된 feature space에서 가장 가까운 이웃을 고려하는 k-nn을 사용한다.
각 layer를 지날 때마다 feature point는 재 구성되며 매번 graph의 형태가 변경된다.
따라서 매번 graph의 형태가 변경되기 때문에 feature를 가장 잘 설명하는 G를 학습한다.

Properties

permutation invarance
- 해당 식의 output과 point feature의 최대값은 항상 동일하다.
  - $\text{max}$연산을 사용하여 $h_\Theta$에서 가장 큰 값을 추출하기 때문
- 따라서 symmetric function이기 때문에 입력되는 순열에 불변하다.
$$ x'i=\text{max}{j:(i, j)\in\varepsilon}h_{\Theta}(x_i,x_j) $$
Translation invarance
- Edge function은 변환에 종속될 수 있다.
$$ e'_{ijm}=\theta_m\cdot(x_j+T-(x_i+T))|+\phi_m\cdot(x_i+T)$$ $$=\theta_m\cdot(x_j-x_i)+\phi_m\cdot(x_i+T) $$
- T는 해당 point cloud가 얼마나 이동되었는지에 대한 값이다. 점들에 대한 평행이동값은 소거가 되지만($e_{ijm}=\text{ReLU}(\theta_m \cdot (x_j-x_i)+\phi_m \cdot x_i)$) 비선형변환 수행과정 중 데이터에 맞게 최적화 되는 변수인 $\phi$는 0이 아니면 T가 소거되지 않는다. 따라서 평행이동에 대해 부분적으로 강건하다.
- DGCNN이 평행이동에 대해 반드시 강건해야 하는 이유는 없다. ⇒ graph를 통해 각 point들의 절대적인 위치가 아닌 상대적인 위치에 대해 의존하기 때문에 평행이동에 대해 강건하지 않아도 classification이나 segmentation의 결과에는 영향을 주지 않는다.
- 또한 데이터를 유클리드 공간에 중앙 정렬하는 방식으로 평행이동의 영향을 최소화한다.

Comparison to Existing Methods

DGCNN은 PointNet과 CNN이라는 두 가지 접근 방식과 관련이 있다.
PointNet 계열 모델은 k=1이라는 특수한 경우로 edge function이 없다고 가정한다. PointNet은 global feature를 고려하지만 local feature를 고려하지 않고 PointNet++은 local feature를 고려하기 위해 FPS 알고리즘을 사용한다. 하지만 layer를 거치며 사용하지 않는 point를 버리게되고 결국 graph의 크기가 작아지게 된다. 또한 PointNet++는 point 간 유클리드 거리를 계산하여 maxpooling 하기 때문에 graph가 고정되고 집계연산도 최대값으로 지정된다.
그래프 CNN에서 MoNet과 ECC는 그래프를 사용한 CNN 연산을 정의할 수 있는 비슷한 형식의 point cloud 연산 모델이다. 하지만 모두 고정된 graph를 사용하여 의미를 전달하지 못하는 한계점을 가지고있다.

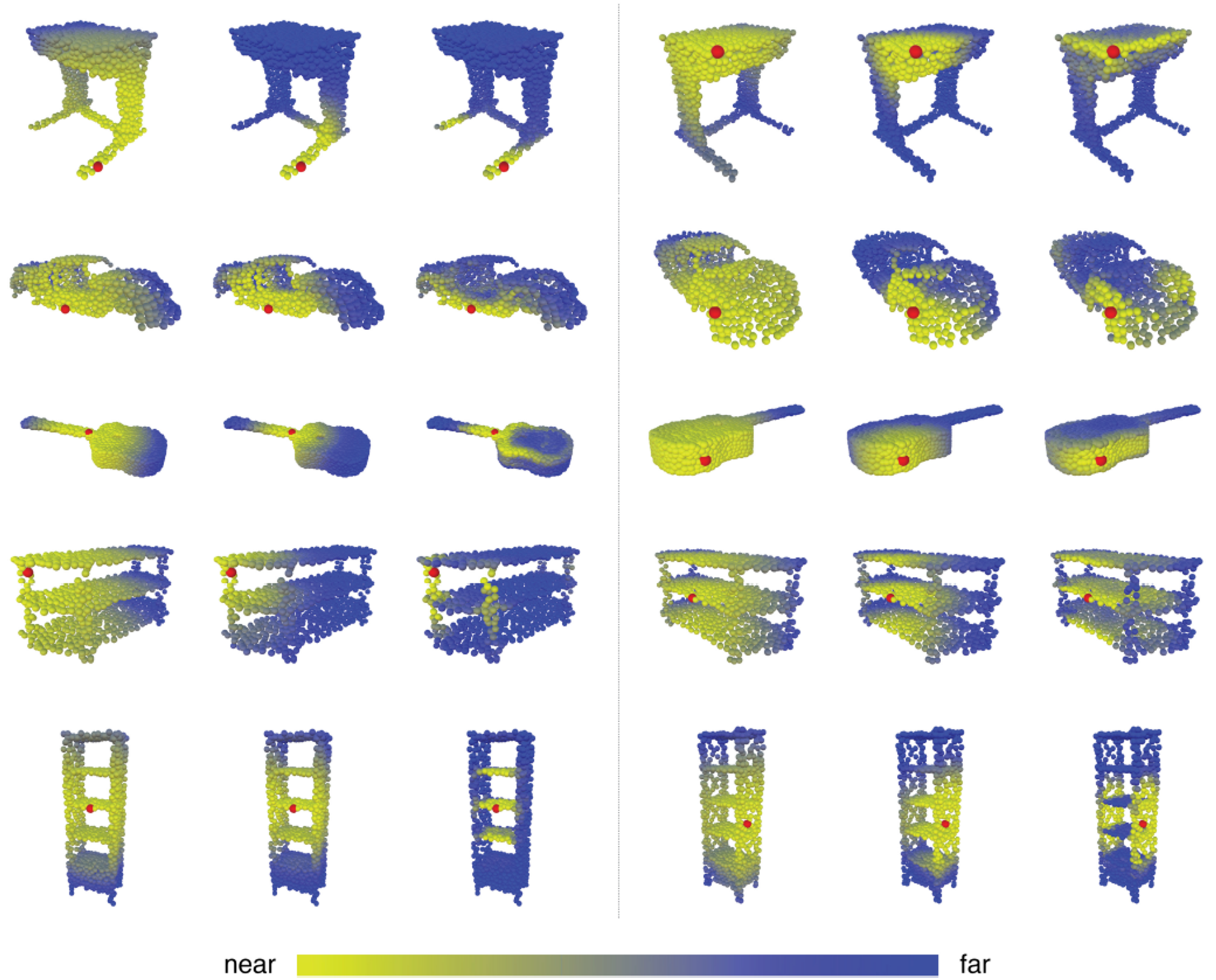
빨간색 점은 G의 한 노드이고 layer를 거듭하며 graph가 변화하고 feature distance를 계산하여 의미적으로 유사한 구조가 원래 공간에서는 멀리 떨어져있지만 part segmentation이 가능하게 되는 과정을 보여준다.

Evaluation

실험은 다음과 같은 단계로 진행된다.
- classification
- model complexity
- part segmentation
- sementic segmentation
- 이전 방법과의 시각화결과

classification

ModelNet40을 사용한다. train과정에서 객체의 크기를 임의로 조정하고 객체와 point 위치를 교란하여 데이터를 증강한다.

해당 architecture를 사용하여 train과 test를 진행한다.

결과는 PointNet보다 더 좋은 성능을 보이고 point의 개수를 2048개까지 늘렸을 때 모든 모델을 압도하는 성능을 보인다.

model complexity

모델 복잡성과 계산 복잡성과 정확도를 측정하였다.

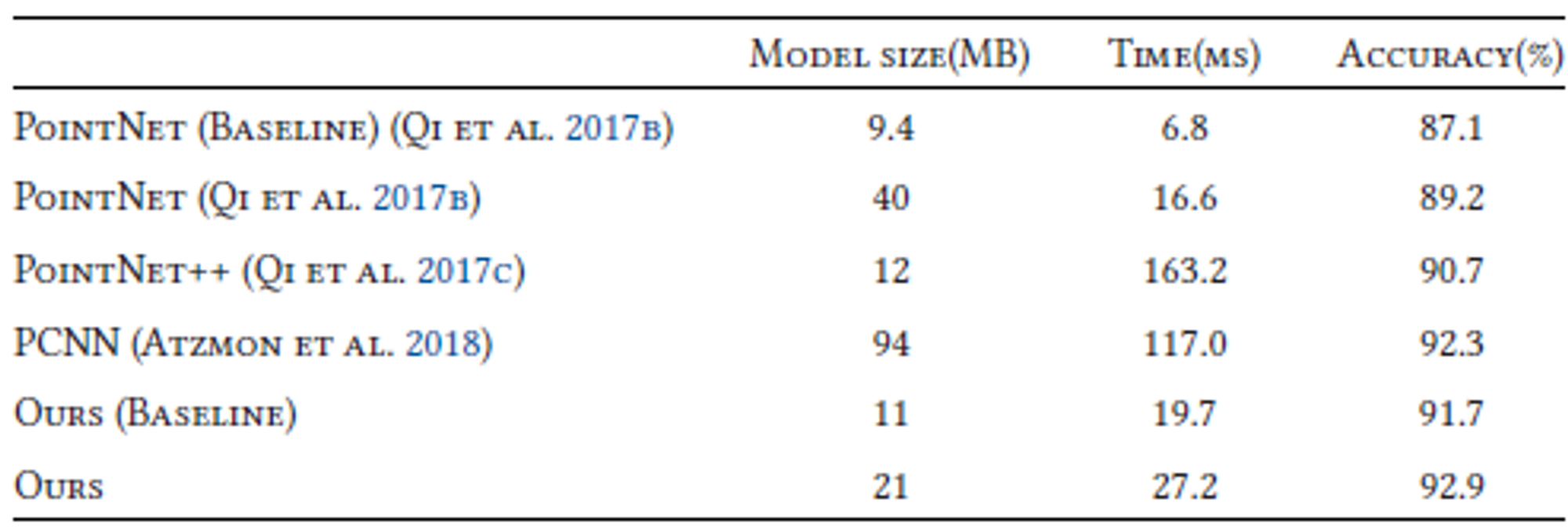
고정된 그래프를 사용하는 모델은 PointNet++보다 정확도가 근소하게 높지만 7배 더 빠르다.
DGCNN은 더 효율적이면서 PointNet++보다 더 좋은 성능과 빠른 속도를 보여준다.

More Experiments on ModelNet40

다양한 모델 설정을 통해 실험을 진행하였다.

중앙 정렬, 동적 그래프 조절, 포인트 증강을 달리하여 실험하였을 때 세 가지 방법 모두 사용한 결과가 성능이 가장 좋았다.
k의 값에 따라서도 같은 실험을 진행하였다.
모든 k의 개수에 대해 실험한 것은 아니지만 k값이 클 수록 성능이 저하된다.
- 이는 특정한 밀도의 경우 k값이 크면 유클리드 거리계산이 잘 되지 않음을 알 수 있고 각 point 간의 거리에 대한 feature를 파괴한다.