카테고리 없음

[논문리뷰]Point Transformer V2: Grouped Vector Attention and Partition-based Pooling

Local Feature 2024. 11. 21. 17:41
반응형

Abstract

  • PTv1에서 사용한 group vector attention보다 더 효과적인 vector attention을 사용하였다.
  • 새로운 group weight encoding layer를 갖춘 group vector attention을 효과적으로 구현하였다.
  • position encoding 방식을 수정하여 position information를 강화한다.
  • 새로운 partition-based pooling 방식을 제안한다.

Introduction

  • PTv1은 self-attention network를 도입하였다.
  • vector attention과 U-Net 스타일의 encoder-decoder를 결합하여 classification, part segmentation, semantic segmentation에서 좋은 성능을 나타낸다.
  • PTv1은 모델이 깊어지고 채널수가 증가함에 따라 weight encoding parameter이 증가하게 된다. ⇒ PTv2는 grouping vector attention을 도입하여 해결하였다.
  • 또한 기존의 vector attention과 multi-head attention의 장점을 모두 계승하였다.
  • PTv1은 2D 방식의 position encoding 방식을 사용하여 3D 좌표에서의 기하학적 정보를 활용하지 못한다. ⇒ PTv2는 relation vector에 추가적으로 position encoding multiplier를 적용하여 강화한다.
  • FPS 알고리즘, Grid Sampling 방식은 시간이 많이 소요되고 point의 공간적 특성을 완벽하게 반영하지 못한다. ⇒ sampling과 query를 조합하여 point cloud를 겹치지 않는 partition으로 나누어 pooling 하는 partition-based pooling 방식을 사용한다

Contribution

  • Group Vector Attention(GVA)를 제안한다.
  • 새로운 position encoding을 제안한다.
  • partition-based pooling을 제안한다.

⇒ Point Transformer V1을 개선하여 새로운 Point Transformer V2를 제안한다.

Related Works

Image transformers

  • ViT가 이미지 처리 분야에서 높은 성능을 달성한 이후 NLP task에서 활용되던 transformer를 다른 분야에도 도입하기 시작하였다.

Point cloud understanding

  • 3D point cloud의 feature를 이해하는 것은 projection, voxel, point 기반 네트워크를 사용하는 방법이 주를 이루었다.
  • Point Transformer V1에서는 이러한 방식이 아닌 attention 기반 네트워크를 사용하여 새로운 해석 방식을 제안하였다.

Point cloud transformers

  • point cloud data를 transformer에 적용하는 연구는 PCT와 Point Transformer V1부터 시작하였다.
  • PCT는 point cloud에 직접 global attention을 적용시켰지만 ViT와 같이 계산비용이 많이 든다는 한계점이 있다.
  • Point Transformer V1은 각 점을 knn 알고리즘으로 묶은 후 local attention을 적용하여 PCT의 계산비용문제를 해결하였다.

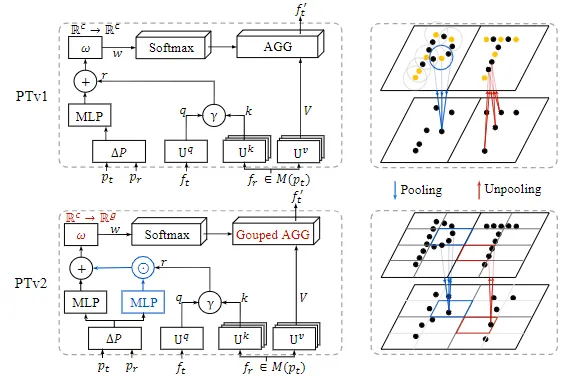
  • 강화된 position encoding : point와 point간의 거리를 미분한 후 query와 key의 vector attention 결과를 hadamard 연산한다.
  • group vector attention : 가중치의 차원을 축소한 후 group vector attention
  • partition-based pooling : 파티션 기반 풀링

Point Transformer V2

3.1 - PTv1의 vector self-attention

3.2 - group vector attention

3.3 - position encoding

3.4 - partition-based pooling

3.5 - PTv2

Problem Formulation and Background

  • M = (P, F)를 point set을 포함하는 3D point cloud로 정의할 때 하나의 point는 $x_i = (p_i, f_i)$로 정의한다.
  • $p_i$는 $(x, y, z)$좌표인 위치를 나타내고 $f_i$는 점의 특징을 나타낸다.
  • semantic segmentation은 각 $x_i$에 대한 class label을 예측하는 것 이다.
  • classification은 각 scene M에 대한 class label을 예측하는 것 이다.
  • local attention
    • scene의 모든 point에서 attention연산을 하는 것은 계산비용이 많이 들기 때문에 실행 불가능하다.
    • swin3d모델은 attention을 겹치지 않는 image grid에 번갈아 적용하는 swin transformer의 개념을 도입하였다.
    • PTv1은 knn 알고리즘에 기반한 neighborhood attention을 채택하였다. point cloud는 항상 밀도가 일관되지 않기 때문에 PTv2는 neighborhood attention을 채택한다.
  • Scalar attention and vector attention
    • 점 $x_i=(p_i, f_i)\in M$이 주어졌을 때 MLP또는 Linear projection을 적용해서 point feature $f_i$를 query, key, value의 feature vector로 projection한다.
    • 각 vector는 channel과 point의 위치 정보를 가진다.

 $w_{ij}=\langle q_i, k_j\rangle/\sqrt{c_h}, \quad f^{attn}_i=\sum_{x_j\in \mathcal{M}(p_i)}\text{Softmax}(w_i)_jv_j$

  • query와 key를 dot product 연산 후 channel 수를 제곱근으로 나누어 가중치가 너무 커지는 것을 방지하며 정규화한다. 이후 해당 가중치를 softmax함수를 통해 정규화하고 비율로 변환한 후 value와 곱해진다. ⇒ 각 point가 이웃한 점들과 얼마나 유사한지 학습하여 point cloud의 feature를 추출한다.
  • Scalar attention 대신 PTv1은 개별 feature channel을 조절할 수 있는 vector attention을 적용한다. vector attention은 weight encoding function이 query와 key의 관계를 vector로 encoding한다.

$w_{ij}=, \omega(\gamma(q_i, k_j))\quad f^{attn}_i=\sum_{x_j\in \mathcal{M}(p_i)}\text{Softmax}(\mathrm{W}_i)_j\odot v_j$

  • weight function은 dot product 대신 관계함수(뺄셈)을 사용한다. 이후 학습가능한 weight encoding(MLP)를 사용하여 계산한다. 이후 해당 가중치를 softmax 함수를 통해 정규화하고 비율로 변환한 후 hadamard product를 사용하여 value와 곱해진다. ⇒ 그림 2(a)는 linear weight encoding을 보여준다.

Grouped Vector Attention

  • vector attention은 layer가 깊어질 수록 parameter의 수는 급격하게 증가한다. 이는 많은 계산비용과 시간을 요구하여 모델의 일반화 성능을 떨어뜨린다.
    • vector attention의 한계점을 개선하기 위해 grouped vector attention을 도입한다.
  • $v \in \mathbb{R}^c$인 value vector의 채널을 $g$ 그룹으로 균등하게 나눈다. 이때 $g$는 $(1 \le g\le c)$
  • weight encoding layer는 c 채널대신 g 채널을 가진 grouped attention vector를 출력한다.

$w_{ij}= \omega(\gamma(q_i, k_j))\quad f^{attn}_i=\sum^{\mathcal{M}(p_i)}_{x_j}\sum^g_{l=1}\sum^{c/g}_{m=1}\text{Softmax}(\mathrm{W}_i)_{jl}v_j^{lc/g+m}$

  • query와 key를 encoding하는 함수이다. $\gamma$는 PTv1과 같은 뺄셈연산이거나 덧셈, 곱셈이 될 수 있다.
  • $f^i_{\text{attn}}$은 각 point에 대한 attention 결과를 나타낸다. 이 point들은 $M(p_i)$집합의 point 들과 연산된다.
  • g는 grouped vector attention을 위한 group을 의미하며 value vector는 g개의 group으로 나뉜다. 하나의 g는 공통된 attention weight를 공유한다. j는 주변 point, l은 group의 인덱스, m은 group내의 인덱스를 의미한다.
  • weight encoding function된 w를 softmax 함수로 정규화하고 주변 point의 group 인덱스들의 값과 channel 인덱스의 value vector를 곱한다. 이후 group으로 나눈 채널 수 만큼 계산하고 전체 합을 구하고 group 수 만큼 sigma 연산, 마지막으로 전체 point만큼 sigma 연산한다.
  • 그림 2(b)는 grouped vector attention을 적용한 예시로 PTv1의 vector attention 보다 더 효율적인 연산을 제공한다.
  • GVA is a generalized formulation of VA and MSA
    • GVA는 group 수와 channel 수가 같을 때 VA가 된다.
    • 식 3에서 w가 다음과 같이 정의된 경우 MSA와 같아진다.
    • $\omega(r) = r \left[ \begin{array}{cccc}
      \mathbf{1}_{1 \times c_g} & \mathbf{0}_{1 \times c_g} & \cdots & \mathbf{0}_{1 \times c_g} \\
      \mathbf{0}_{1 \times c_g} & \mathbf{1}_{1 \times c_g} & \cdots & \mathbf{0}_{1 \times c_g} \\
      \vdots & \vdots & \ddots & \vdots \\
      \mathbf{0}_{1 \times c_g} & \mathbf{0}_{1 \times c_g} & \cdots & \mathbf{1}_{1 \times c_g}
      \end{array} \right]^T \frac{1}{\sqrt{c_g}},$
  • 각 채널들을 나타내기 때문에 행렬형태의 함수로 나타낼 수 있다. 행렬은 $g\times c_g$크기이다.
  • 큰 행렬의 요소는 작은 행렬을 의미한다. $1_{1\times c_g}$는 $c_g$=4 인 경우 [1, 1, 1, 1]이 된다.
  • 큰 행렬에서 하나의 열만 모든 작은 행렬을 1로 만들고 나머지는 0으로 만든다. 그 이유는 query와 key의 계산 결과가 해당 group의 attention에 영향을 주지 않도록 한다. 특정 group에서만 attention이 활성화되어 각 group의 weight를 독립적으로 설정할 수 있도록 한다.
  • channel을 group으로 만들어 적은 수의 파라미터로도 효과적인 학습을 가능하게 한다.
  • channel을 group으로 만드는 것은 개별적으로 연산하는 것 보다 성능이 낮아질 수 있다는 우려가 있으나 특정한 feature를 강조하고 계산 비용이 줄어들기 때문에 성능저하를 보완할 수 있다.
  • 전치행렬로 변환하여 다른 행렬들과의 dot product나 hadamard product를 더 용이하게 만들 수 있다.
  • Grouped linear
    • MSA의 weight encoding function을 변형시켜 각 group이 서로 다른 파라미터로 학습할 수 있도록 한다.
    • PTv2의 weight encoding function은 group linear layer, Normailized layer, Activate layer으로 구성된다.
    • $\zeta(r) = r \left[ \begin{array}{cccc}
      p_1 & \mathbf{0}_{1 \times c_g} & \cdots & \mathbf{0}_{1 \times c_g} \\
      \mathbf{0}_{1 \times c_g} & p_2 & \cdots & \mathbf{0}_{1 \times c_g} \\
      \vdots & \vdots & \ddots & \vdots \\
      \mathbf{0}_{1 \times c_g} & \mathbf{0}_{1 \times c_g} & \cdots & p_g
      \end{array} \right]^T$ 
  • MSA와 달리 1로 통일되는 작은 행렬들이 아닌 모두 다른 가중치를 가지는 $p$를 큰 행렬에 표기한다. 이후 Normailized layer, Activate layer, group linear layer를 거치고 weight를 추출한다.

Position Encoding Multipler

  • 3D point cloud는 이산적이지 않고 연속적이다, 또한 유클리드 공간 내에서 밀도가 고르지않다.
  • PTv1은 단순히 $p_i$와 $p_j$의 좌표를 빼서 위치정보를 계산한다.
  • PTv2는 관계벡터(뺄셈)에 추가적인 multipler를 사용하여 position encoding을 강화한다.

$w_{ij}=\omega(\delta_{mul}(p_i-p_j)\odot \gamma(q_i, k_j)+\delta_{bias}(p_i-p_j))$

  • $\delta_{mul}$은 point 간의 위치 차이와 query, key 계산 결과를 hadamar product로 계산한다. 이후 point의 위치 차이에 대한 편향함수인 $\delta_{bias}$를 더해준다.
  • 강화된 position encoding은 연속적인 3D point cloud 공간에서 더 효율적이고 모델의 point cloud 인식 성능을 향상시킨다.
  • $\delta_{mul}$과 $\delta_{bias}$는 MLP layer를 통과하며 계산된다.
  • pos, key = key[:, :, 0:3], key[:, :, 3:]
  • 첫번 째 차원은 batch size(size of input sample)를 나타내고 두 번째 차원은 head 수를 나타낸다. 따라서 마지막 차원의 0부터 2까지의 위치 정보를 가져오기 위해 다음과 같은 코드를 사용한다.

Partition-based Pooling

  • 기존의 sampling 방식은 FPS 알고리즘이나 grid sampling을 사용한다. ⇒ 각 query set 간 정보의 불균일한 밀도와 중복된 set를 포함하기 때문에 성능이 낮다는 한계점이 있다.
  • Pooling
    • point set $M$이 주어질 때 공간을 겹치지 않는 partition으로 나누어 $M=[M_1, M_2,\dots, M_n]$인 부분집합으로 분할한다. 이후 하나의 부분집합 $M_1$을 다음 식과 같이 융합한다.

$f'_i=\text{MaxPool}(\{f_jU|f_j\in\mathcal{F}_i\}),\qquad p'_i=\text{MeanPool}(\{p_j|p_j\in\mathcal{P}_i\})$

  • $f'$는 feature, $p'$는 position을 의미한다. feature는 전체에서 가장 두드러진 feature를 선택하여 다음 연산으로 넘겨주는 것이 중요하기 때문에 Maxpooling하고 position은 각 point들의 평균적인 positon을 구해야하기 때문에 Meanpooling한다.
  • $U$는 grouped linear layer를 의미한다. 수학적인 linear transform 중 모델에서 사용한 grouped linear layer을 사용한다.
  • 해당 연산과정을 거치게되면 다음 encoding 단계에서 사용할 point set을 만들 수 있다.
  • gird pooling과 유사하기 때문에 partition-based pooling은 gird pooling이라고도 부른다.
  • UnPooling
    • 보간법에 의한 unpooling은 partition-based pooling에도 적용될 수 있다.
    • 원래 point feature가 특정 그룹인 $M_j$에 포함된 경우 가장 큰 값을 설정하였기 때문에 그 값과 같은 값을 $f_i^{up}$로 설정해도 무방하다.

$f^{up}_i=f'_j,\qquad \text{if}(p_i, f_i)\in \mathcal{M}_j$

Network Architecture

  • PTv1와 Minkowski network와 같이 skip connection 구조를 가진 U-Net을 채택한다. 이후encoder와 decoder는 [2, 2, 6, 2]와 [1, 1, 1, 1]의 블록 깊이를 가진 단계로 구성되며 partition의 크기 배수는 [x3.0, x2.5, x2.5, x2.5]으로 확장된 비율을 나타낸다.
  • attention은 PTv1과 같이 local neighborhood에서 수행된다.
  • segmentation을 위해 point feature를 input point에 개별적으로 mapping 하기 위해 MLP layer를 통과시킨다.
  • classification을 위해 point feature를 global average pooling 하고 MLP classifier를 통해 분류한다.

Experiments

Semantic Segmentation

  • PTv2의 성능평가를 위해 Semantic Segmentation에서는 ScanNetv2와 S3DIS를 사용한다.
  • PTv2의 성능평가를 위해 Classification에서는 ModelNet40을 사용한다.

  • 두 개의 dataset에서 모두 가장 높은 성능을 달성하였다.
  • PTv2는 더욱 세부적인 사물의 구조를 포착하는 것을 알 수 있다. 예를 들면 의자의 다리와 팔걸이까지도 segmentation을 수행한다.

Shape Classification

  • PTv2는 classification task에서도 높은 성능을 달성하였다.

Ablation Study

  • Attention type
    • 두 가지 유형의 local attention인 shift grid attention과 neighborhood attention을 실험한다.
    • GVA와 MSA를 비교한다.
    • Neighborhood와 GVA를 결합한 방식이 가장 성능이 높은 것을 알 수 있다.
    • 균일하지 않은 공간에서는 shifted-grid attention보다 Neighborhood attention이 더 성능이 높고 group에 따라 channel group의 파라미터를 다르게 설정한 것이 더 성능이 높다고 해석할 수 있다.

  • Weight encoding
    • multi-head scalar attention weight encoding function : MSA
    • Linear layer : L
    • Grouped linear layer : GL
    • BatchNorm, Activation, Linear layer : L+N+A+L
    • Grouped linear layer, BatchNorm, Activation, Linear layer : GL+N+A+L
    • GL은 MSA 보다 근소하게 우수한 차이를 보인다. 그러나 grouped 간 정보를 교환하는 방식과 정규화, 활성화 방식을 결합하면 MSA 방식보다 더 향상된 결과를 얻을 수 있다.

  • Pooling methods
    • FPS 샘플링 보다 partition-based pooling 방식이 전체적으로 성능이 더 높다.
    • 초기에 partition을 작게 잡는 것이 성능이 더 높아진다.
    • 하지만 grid 크기 배율이 전체 성능에 큰 영향을 미치지 않기 때문에 계산 비용의 감소를 위해 gird 크기 비용을 더 크게 만들 수 있다.

  • Module design
    • PTv2에서 사용한 GVA, Position Encoding Module, Grid Pooling, Mapping Unpooling을 제거하는 연구를 진행하였다.
    • 모든 방식을 사용한 모델이 가장 성능이 높다.

Model Complexity and Latency

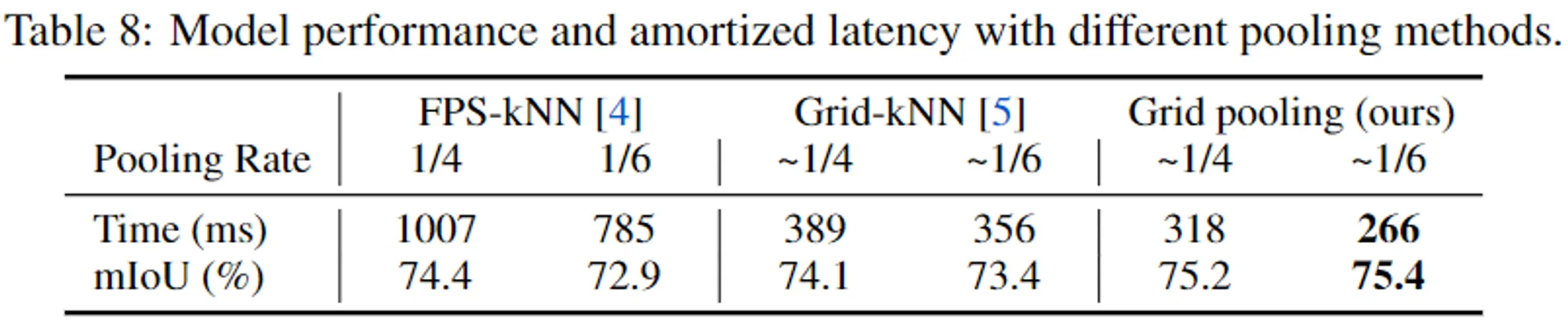
  • Pooling methods
    • 다양한 pooling 방법과 시간, 성능을 보여준다.
    • gird pooling이 가장 시간이 적게 걸리고 성능이 높다.

  • Module design
    • 모든 방식을 적용한 것이 PTv1과 비교하였을 때 시간이 가장 적게 걸리고 성능이 높다.
    • position encoding multipler이 유일하게 계산 비용을 높이지만 성능이 향상된다.

Conclusion

  • PTv2는 PTv1보다 더 높은 성능을 가짐과 동시에 더 경량화된 모델이다.
  • 향후 연구로는 더 강건하고 간단하고 빠른 모델을 제시할 예정이다.
반응형
저작자표시 비영리 변경금지

'카테고리 없음'의 다른글

  • 현재글[논문리뷰]Point Transformer V2: Grouped Vector Attention and Partition-based Pooling

티스토리툴바